Oltre le top-k: skyline queries

data una relazione $R(A_1,A_2,...,A_m,...)$ dove $A_i$ sono gli attributi di rank una tupla $t$ domina una tupla $t^{'}$ ($t \succ t^{'}$) quando
$$\forall j \in [1,m] t_{Aj} \leq t^{'}_{Aj} \land \exists j: t_{Aj} \lt t^{'}_{Aj}$$

ovvero $t$ ha valori non peggiori di $t^{'}$ e almeno un valore di $t$ e strettamente migliore di $t^{'}$

Si definiscono di conseguenza le regioni di dominanza e anti-dominanza di una tupla $t$

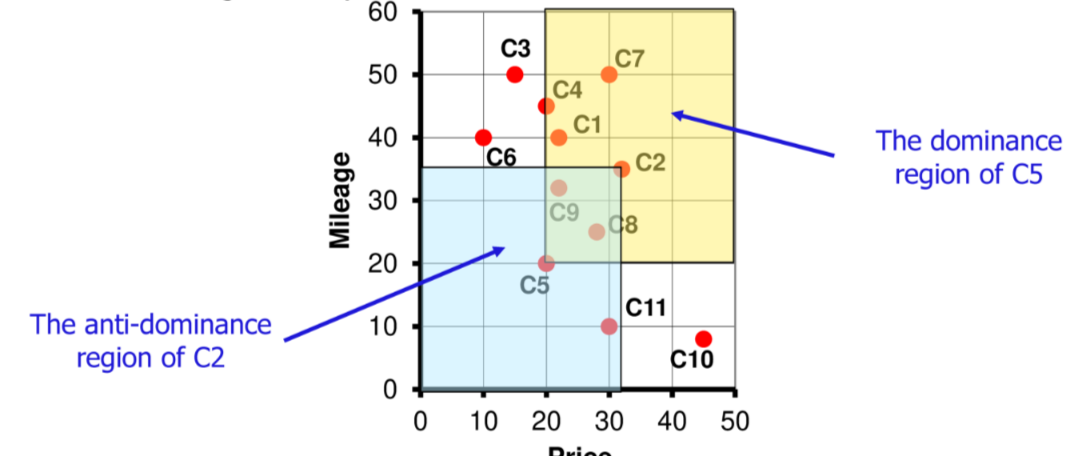
Di conseguenza l’output della skyline query e definito come segue:

data una relazione $R(A_1,A_2,...,A_m)$ la sua skyline e definita come
$$sky(R) = \{t | t \in R, \nexists t^{'} \in R: t^{'} \succ t\}$$

Cosa c’e’ di speciale nelle query skyline
#

Se si prende in considerazione il set di funzioni di distanza monotone $MD$ si ha che il primo nearest neighbor per una funzione di distanza $d$ e parte della skyline e che un punto della skyline $t$ e minimizza sempre una qualche funzione di distanza $d \in DM$

$$ t \in sky(R) \Leftrightarrow \exists d \in MD: \forall t^{'} \in R, t^{'} \neq t: d(t,q) \lt d(t^{'},q) $$

Inoltre l’output della query skyline non corrisponde a quello di nessuna query top-$k$

Data una relazione $R(A_1,...,A_m)$ non esiste nessuna funzione di distanza $d$ che per tutte le istanze possibili di $R$ contiene tutti i punti della skyline nelle prime $k$ posizioni

💡 Quindi la skyline ha più potere espressivo

Valutare le query skyline
#

Il problema con la valutazione delle query skyline sta nel fatto che nel caso peggiore la complessità segue $\Theta(N^2)$ per un database con $N$ oggetti, i possibili approcci sono i seguenti:

computare la skyline sfruttando una scansione sequenziale del file
sfruttare un indici

Naive nested loops
#

La soluzione più semplice e quella di scandire $R$ per comparare una tupla con tutte le altre

Sky = []
for t in R:
	undominated := true;
	# comparazione con tutte le tuple di R
	for c in R:
		if c.dominates(t):
			undominated = False
			break
	# aggiunge la tupla se non dominata
	if undominated:
		Sky.append(t)
retun Sky

❗ non molto efficiente…

Block nested loops
#

Un miglioramento lo si ha sfruttando un blocco di memoria di dimensione $w$ e ogni tupla letta dal file viene comparata con quelle nel buffer e di conseguenza scartata se non dominante

Performance del block nested loops
#

Evidenze sperimentali hanno dimostrato che BNL e CPU intensive e con un basso costo di I/O, inoltre la dimensione $w$ della window degrada le performance in quanto si effettuano più controlli sulle tuple

Sfs sort-filter-skyline
#

L’idea e quella di ridurre il numero di confronti, per fare ciò si introduce un ordinamento topologico completo che garantisce che

$$t \succ t^{'} \Rightarrow t \lt t^{'}$$

in questo modo si ha che una tupla letta non può dominarne una già letta

Questo approccio ha diversi vantaggi tra cui:

non si effettuano comparazioni tra punti non della skyline
le tuple nella window possono essere date in output subito in quanto non ci sono tuple nel file in grado di dominarle
viene effettuato il minor numero di iterazioni $\lceil |\frac{sky(R)}{W}|\rceil$

Salsa sort and limit skyline algorithm
#

SaLSa e un miglioramento di SFS in quanto se le tuple sono ordinate topologicamente non e necessario leggere tutto il file, il punto di arresto e stabilito quando nessuna tupla e nell’area di dominanza di un dato stopping point $t_{stop}$ in particolare si ha che la scelta ottimale e data da

$$ t_{stop} = argmin_{t \in sky(R)}(max_i(t_{Ai}))$$

ovvero il punto della skyline per cui la coordinata maggiore e minima

Computare la skyline con r-tree
#

L’idea di base sta nel non accedere a nodi che rappresentano aree completamente dominate da punti della skyline

#Input: index tree with root node RN
#Output: Sky, the skyline of the indexed data
PQ = TreeRoot
Sky = []
while ! PQ.empty():
	node = pq.next()
		for t in sky:
			dominate = False
			if t.dominates(node):
				dominate = True
		if  ! dominate:
		if node.isTuple():
			sky.append(node)
		else(PQ.append(node.childs))
return Sky

💡 l’algoritmo BBS e ottimale e corretto :)

Skyline in domini a bassa cardinalita
#

Molte situazioni reali prevedono che gli attributi di interesse per la skyline abbiano un numero limitato di valori (booleani o enumerazioni)

In questo caso si possono sfruttare le peculiarità di questi domini

Algoritmo ls-b
#

Viene predisposta una matrice data da tutte le possibili combinazioni degli attributi di interesse

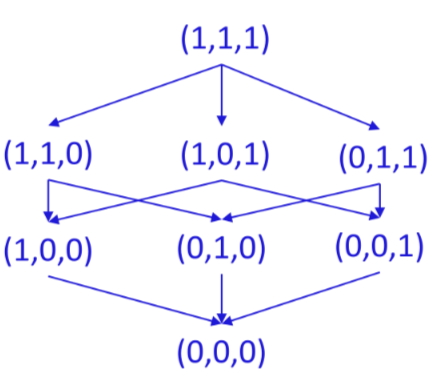
Si scandisce il file e si marcano le tuple corrispondenti nella matrice come presenti, successivamente si determinano le dominanti tra quelle presenti e si rilegge il file fornendo in output quelle nella matrice