Lambda calcolo

Nasce contemporaneamente alla macchina di Turing con l’obbiettivo di descrivere ogni algoritmo (Turing-equivalente), e basato sul solo concetto di funzione

Sintassi e semantica

#

dove $L$ può esprimere qualunque struttura dati e qualunque algoritmo

$\rightarrow$ invece rappresenta una trasformazione atomica che applica la sostituzione di testo, ovvero nella espressione

La semantica risulta essere sostituisci tutte le occorrenze del parametro $x$ nel corpo della funzione $x$ con risultato $y$, l’operazione e detta riduzione

Notare che la grammatica cosi definita e ambigua e derivazioni diverse di una stessa frase portano a semantiche diverse, per esempio la frase

può essere interpretata come:

applicare il parametro $y$ alla funzione di corpo $x$ e parametro formale $x$ $\lambda (x.x)y$

oppure:

funzione di parametro $x$ e corpo $xy$ $\lambda x.(xy)$

Lambda calcolo in javascript

#

javascript risulta essere pratico per l’implementazione del lambda calcolo in quanto vi e la possibilità di definire funzioni anonime e chiusure

//il termine lambda x.<expr> puo infatti essere definito come

f = function (x){return x;}//per semplicita eseguiamo la funzione identita
//mentre la chiamata puo essere interpretata come una chiamata di funzione stessa
y=5
console.log(f(y))

Funzioni a più argomenti

#

Funzioni a piu argomenti possono essere rappresentate come funzioni di funzioni sfruttando il currying, di conseguenza una funzione a piu argomenti:

Viene interpretata come una funzione di parametro $x$ e corpo una funzione di parametro $y$ e corpo $xy$

Funzioni notevoli

#

Esistono alcune funzioni notevoli cosi definite:

• $I ::=\lambda x.x$
• $K ::=\lambda x.\lambda y.x$
• $S ::=\lambda n.\lambda z.\lambda s(nzs)$
• $\omega ::=\lambda x.xx$
• $\Omega ::=\omega\omega = (\lambda x.xx)(\lambda x.xx)$

ℹ️ l’operatore $\Omega$ riproduce sempre se stesso

Forma normale

#

Un lambda termine e in forma normale se non si possono applicare riduzioni ulteriori, ma dato che la grammatica e ambigua questa proprieta dipende dall’ordine di riduzione

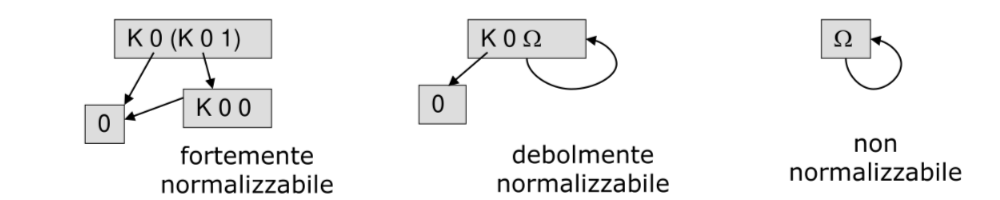
• lambda termine fortemente normalizzabile se qualunque ordine di riduzione porta a una forma normale

f= function(x,y){ return x+y+1; }
console.log(f(2,4))

• lambda termine debolmente normalizzabile se almeno un ordine di riduzione porta a una forma normale

f=function(x){ return x==0 ? 0 : f(x); }
console.log(f(0))

💡 qui funziona perche il parametro attuale e $0$

• lambda termine non normalizzabile se nessun ordine di riduzione porta a una forma normale

f=function(x){ return f(x); }
f(2)

esplode lo stack, ovviamente

Teorema di church-rosser

#

Ogni lambda termine ha al piu una forma normale

Da questo si deriva che il lambda calcolo e deterministico, i grafi hanno una e una sola foglia (se sono aciclici)

Logica booleana con il lambda calcolo

#

Per rappresentare la logica booleana sono necessari:

• due valori distinti per TRUE e FALSE
• le operazioni AND OR NOT

Che in lambda calcolo divengono:

• T= $\lambda x.xy$
• F= $\lambda x.yy$
• NOT=$\lambda x.xFT$
• AND=$\lambda x.\lambda y.xyF$
• OR=$\lambda x.\lambda y.xTy$

che in javascript diventa:

//uso pesante del curring come discusso prima
t = function(x) { return function(y) { return x; }}
f = function(x) { return function(y) { return y; }}
n = function(x) { return x(f)(t) }
a = function(x) { return function(y){ return x(y)(f); }}
o = function(x) { return function(y){ return x(t)(y); }}
console.log(n(t))
console.log(n(f))
console.log(a(t)(f))
console.log(o(t)(f))

ℹ️ notare che i simboli T e F sono esistessi definiti come termini funzione, anche se riducibili, a testimonianza del fatto che il lambda calcolo e capace di rappresentare qualunque struttura dati e algoritmo con un solo formalismo sintattico :)

Strategie di riduzione

#

Come mostrato prima la procedura di riduzione non e detto porti sempre a una forma normale, e pertanto importante determinare la strategia con cui si decide di ridurre la frase:

Strategie eager

#

Basate sul concetto di sviluppare il prima possibile i termini sulla destra

• Applicative order (rightmost innermost)
• Call by value
• Call by reference
• Call by copy-restore

Strategie lazy

#

Basate sul applicazione dell’argomento alla funzione piuttosto che alla risoluzione dell’argomento stesso

• Normal order (leftmost outermost)
• Call by name
• Call by need
• Call by macro

Turing equivalenza

#

Il lambda calcolo e Turing equivalente, ovvero e in grado di rappresentare

• i numeri naturali
• il concetto di successore $succ(n)=n+1$
• il concetto di proiezione $f(x,y)=y$
• il concetto di composizione $f(g(x))$
• la ricorsione

Ricorsione nel lambda calcolo

#

Per poter rappresentare la ricorsione e necessario poter richiamare le funzioni per nome, tuttavia nel lambda calcolo le funzioni sono anonime ergo questo non e possibile.

Si introduce quindi il concetto di operatore di punto fisso $Y$ che e cosi definito

Che applicato a una funzione ha l’effetto di ‘rigenerarla’

Si dice infatti che $YF$ e un punto fisso per la funzione $F$

ℹ️ l’operatore di punto fisso e possibile solo se si adotta come strategia di riduzione la call by name in quanto le altre strategie divergerebbero

function Y(f) {
	return (
	//con la call by value si cerca di valutare x all'infinito
	(function(x) {return f( x(x) ); })
	(function(x) {return f( x(x) ); })
	);
}

E necessario simulare la call by name come già visto

Combinatore di punto fisso rivisitato $z$

#

Per poter operare con la call by value e necessario ridefinire l’operatore di punto fisso come segue

Che in javascript si traduce

function Z(f) {
	return (
		(function (x) {
			return f( function(v){ return x(x)(v); } ); })
		(function (x) {
			return f( function(v){ return x(x)(v); } ); })
	);
}

Implementazione della ricorsione

#

Dato l’operatore di punto fisso per ricreare la ricorsione e necessario:

• definire una funzione di ordine superiore che abbia come punto fisso la funzione $f$ che si desidera rendere ricorsiva

• separare la business logic della funzione ricorsiva in un altra funzione $step$

• lasciar gestire al combinatore di punto fisso la ricorsione

Di seguito un esempio con il calcolo del fattoriale

// Z utilizzato per gestire la call by value
function Z(f) {
	return (
		(function (x) {
			return f( function(v){ return x(x)(v); } ); })
		(function (x) {
			return f( function(v){ return x(x)(v); } ); })
	);
}
//funzione di ordine superiore con la business logic come punto fisso
FactGen = f => x => (x==0) ? 1: x*f(x-1)
console.log(Z(FactGen)(3))

In conclusione

#

Il lambda calcolo e un formalismo estremamente potente che ha permesso di formalizzare le funzionalità che oggi vantano i linguaggi mainstream ma non e pensato per essere utilizzato direttamente dagli utenti finali