L’azione di sort dei dati non e un operatore dell’algebra ma risulta molto utile per risolvere alcune situazioni tra cui query ORDER BY, bulk loading degli indici e operatori di JOIN e GROUP BY.
Gli algoritmi di sort possono essere suddivisi in base alla memoria in cui vengono svolti:
| algoritmi di sort interni | algoritmi di sort esterni |
|---|---|
| eseguiti in memoria centrale, con prestazioni molto buone | eseguiti usando la memoria secondaria di appoggio |
Merge sort esterno #
Il concetto alla base di questo sistema di sorting e caricare i dati in memoria centrale in sequenze (dette run), ordinarle con un merge interno e poi eseguire il merge una per volta
ℹ️ il primo passo di ordinamento utilizza un sort interno
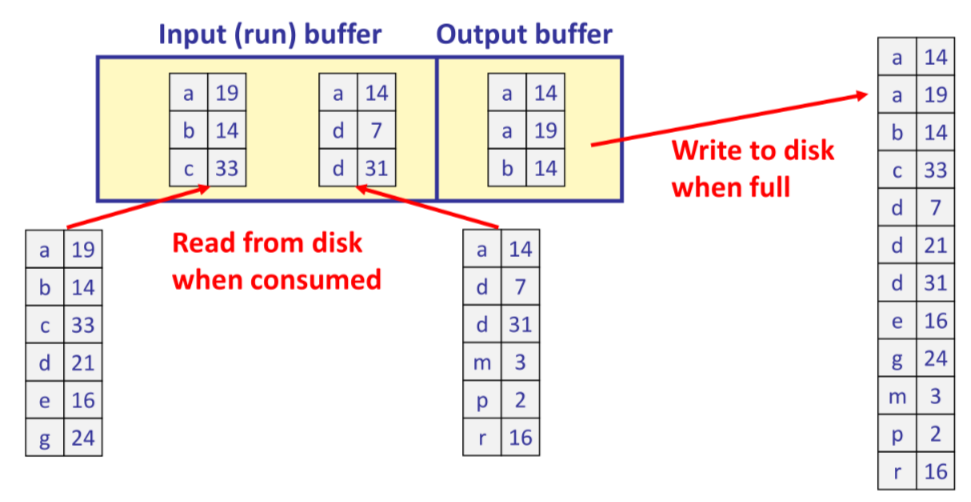
Nella fase di fusione vengono usati 3 buffer (uno per l’output) dove vengono caricati in input le pagine delle run e mergiate nella pagina di output
Merge sort esterno: performance #
dato un numero di pagine in input $P=2^k$ il numero di passi dell’algoritmo di sort merge e $\lceil \log_{2}{P}\rceil +1$ con un costo totale (in numero di letture scritture) $2P(\lceil \log_2P\rceil +1)$. Con $P = 8192$ e tempo di I/O $10ms$ si ha un costo di $38$ minuti
direi non il massimo…
Migliorando il sort merge: sort merge a z vie #
Un possibile miglioramento consiste nell’utilizzare $Z+1$ buffers (uno sempre per l’output) nella fase di merge, aumentando il fan-in della fase di merge
Determinare il valore di $z$ #
La scelta più immediata per determinare il valore di $Z$ sarebbe farlo più grande possibile cosi da massimizzarne il vantaggio, tuttavia questo a 2 limitazioni principali:
- consumo di CPU, in quanto il costo di determinare il maggiore fra $Z$ elementi segue $O(Z)$
- non vi e distinzione tra letture random e sequenziali del disco
Distinguendo tra i due tipi di letture si ha che:
$$ costo \space letture \space sequenziali = (C + X)T_t $$$$ costo \space letture \space random = X(C + 1)T_t $$
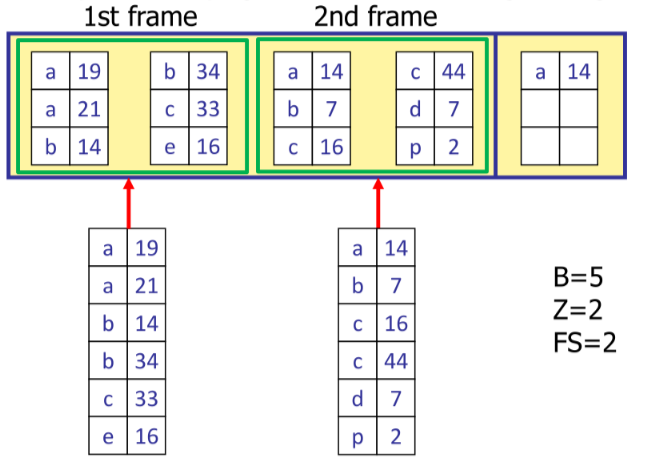
Di conseguenza si possono organizzare le letture delle pagine in batches detti $Z$-frame da $FS$ pagine ciascuno
Sorting con b+tree #
Nel caso di ordinamento con b+tree e necessario distinguere tra le tipologie di indice
- se l’indice e clustered il costo e dato dal numero di foglie e di pagine del file dati (costo $L+P$)
- se l’indice e un-clustered ogni record causa l’accesso al file dati (costo $L+N$), se gli attributi interessanti sono contenuti nell’indice si può evitare di accedere al file dati (costo $L$)
