Ricerca del piano di accesso

Uno degli approcci più diffusi per stimare la cardinalità di un dato operatore su una relazione e quello di tenere informazioni statistiche sulle relazioni all’interno dei cataloghi, per esempio DB2 mantiene le seguenti informazioni

FPAGES pagine usate dalla table ($P$)
NPAGES pagine contenenti record ($\leq P$)
CARD record di una table ($N$)

Per gli attributi:

COLCARD numero valori distinti per attributo ($NK$)
HIGH2KEY secondo valore maggiore
LOW2KEY secondo valore minore

Determinare la selettività di un predicato
#

Come visto prima e fondamentale determinare la selettività di un predicato per stimarne i record in output, assumendo una distribuzione uniforme dei valori degli attributi

predicato	Fattore di selettivita
$A = v$	$f = 1/NK(A)$
$A \space in \space (v_1,...,v_n)$	$f = n/NK(A)$
$A \lt v$	$f = \frac{v - min(A)}{max(A)-min(A)}$
$A \space between \space v_1 \space and \space v_2$	$f = \frac{v_2 - v_1}{max(A) - min(A)}$

Selettività in caso di più operatori
#

In caso di combinazione di operatori se si conoscono le selettività dei singoli operatori si può stimare la combinazione come

$$ f = f_1 \times f_2 \times f_3 \times ... \times f_n $$

❗ La cosa e più complessa se si hanno i fattori combinati degli operatori

Selettività del join
#

La selettività del join si stima come $f_j*N(R)*N(S)$, in caso di equi join si assume che tutti i valori dell’attributo di join della relazione con meno valori si mappino in una tupla di output quindi si ha

$$ f_j = \frac{1}{max(NK(R.A),NK(S.B))} $$

💡 nel caso di chiave primaria si ha che la cardinalità e pari a $N(S)$ dato che $f_j = \frac{1}{N(R)}$

Cardinalità della proiezione
#

Se si proietta su un attributo solo di $A$ si ha che $E = NK(A)$
Se si proietta su un attributo chiave o non si hanno informazioni si ha il caso peggiore $E = N(R)$

Stimare i valori distinti
#

Una delle metriche più fondamentali da stimare e il numero di valori distinti di un attributo $NK(A)$, le strategie per la stima sono le seguenti

collezionare statistiche accurate

troppo costoso

campionare i dati
usare metodi hash con modelli probabilistici (alla cardenas )

Linear counting
#

Una delle modalita di stima per mezzo di modelli probabilistici e quello di predisporre un array di $B$ bit e una funzione hash a $[0,B-1]$ si scandisce la relazione e si applica la funzione di hash all’attributo in questione

flowchart LR A[(R)] subgraph central memory B[funzione hash] C[B_0] D[B_1] E[B_n] end A --> B -- H --> C & D & E

il numero di valori distinti viene quindi stimato come $NK(A) = Bln(B/Z)$

Superare l’ipotesi della distribuzione uniforme: istogrammi
#

Fino ad ora si e dato per ipotesi che i dati di un dato attributo fossero distribuiti in maniera uniforme ma nella realtà questo e un caso molto raro, per superare questa limitazione si fa l’utilizzo di istogrammi

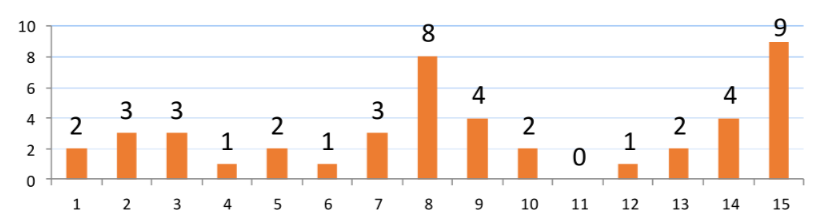
Istogrammi: tipologie
#

Ci sono diverse tipologie di istogrammi

equi-width il dominio e suddiviso in $B$ intervalli della stessa ampiezza facile da aggiornare ma non si hanno garanzie sull’errore della stima
equi-depth i bucket sono divisi in modo che il numero di tuple per intervallo sia simile
equi-compressed estensione degli istogrammi equi-depth dove viene mantenuto un contatore a parte per il valore piu frequente (MVC)

Ottimizzare query su una relazione
#

In caso di query su una singola relazione (presente una sola tabella nella clausola FROM) e necessario gestire solo selezioni e proiezioni, ci sono 4 casistiche possibili:

Scansione sequenziale
Uso di un solo indici (eventualmente clustered)
Uso di più indici
Uso solo di un indice (non si accede ai dati)

Ottimizzare query con più relazioni
#

In caso di relazioni multiple e necessario comprendere come ordinare le operazioni di join , date le sue proprietà lo spazio di ricerca e esponenziale nel numero $n$ di relazioni

Date $n$ relazioni il numero di possibili join trees sono dati da

$$ JT_{n+1} = \frac{2n!}{n!} $$

Se si considerano anche tutte le possibili implementazioni di join si deve aggiungere un fattore $m^n$

lo spazio di ricerca cresce esponenzialmente

Programmazione dinamica
#

La tecnica più utilizzata per ridurre lo spazio di ricerca e basata sul principio di ottimalita

dati 2 percorsi parziali $P_1$ e $P_2$ che hanno origine in $S$ e arrivano entrambi in un nodo $V$, se $costo(P_1) \lt costo(P_2)$, allora $P_2$ non può essere esteso in modo tale da generare un percorso di costo minimo da $S$ a $T$

Questo permette di ignorare tutti i percorsi figli di uno non ottimale

Algoritmo dp
#

L’algoritmo sfrutta il principio di ottimalita per escludere ad ogni passo i piani non ottimali:

primo passo: viene determinato il piano parziale migliore per tutte le relazioni
passo $k$-esimo per ogni sottoinsieme di $k$ relazioni viene determinato il piano migliore a partire dai piani selezionati al passo $k-1$

ℹ️ l’output non considera gli operatori di accesso fisico ai dati

Programmazione dinamica, ridurre lo spazio di ricerca
#

Lo spazio di ricerca dell’algoritmo e comunque esponenziale in $n$, e dunque necessario adottare euristiche che consentano di ridurre lo spazio di ricerca, le strategie più adottate sono

escludere i prodotti cartesiani
considerare solo left-deep join trees

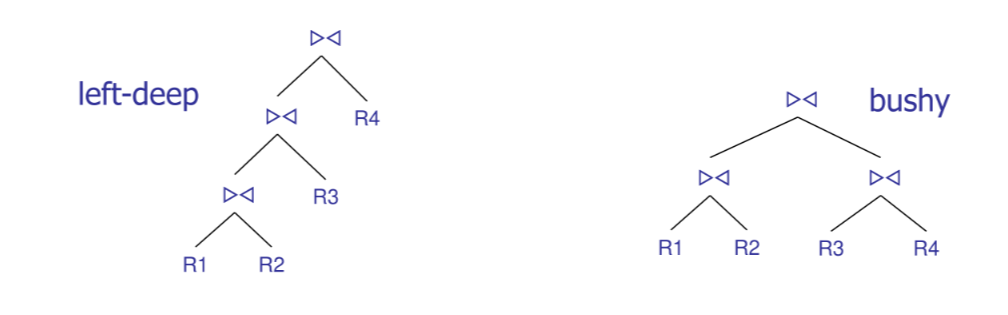
In caso di utilizzo esclusivo dei left-deep join trees lo spazio di ricerca si riduce a

$$ JTLD\_DP_n = \sum_{k=1}^{n} \binom{n}{k} = n \times 2^{n-1} $$

Greedy join enumeration
#

Per ridurre ulteriormente lo spazio di ricerca si sceglie il join che ha costo minimo (a parita, quello che produce meno tuple in output)

Ordini significativi
#

Si dice che l’ordine delle tuple di un operatore e significativo se può influenzare le operazioni che restano da compiere per una query

SELECT S.snome, R.rivista, V.cantina
FROM Recensioni R, Sommelier S, Vini V
WHERE R.vid=V.vid
AND R.sid=S.sid
AND V.vnome='Merlot'
ORDER BY S.snome,V.cantina

In questo caso se si sceglie di eseguire il join prima tra $V$ ed $R$ l’ordine significativo sarebbe quello su $sid$, se le tuple fossero ordinate per $snome$ e $cantina$ sarebbe l’ordine più significativo in quanto risolve ORDER BY

Se si considerano gli ordini significativi e necessario estendere la definizione precedente come segue

Un piano di accesso (parziale) $AP$ per un sottoinsieme di relazioni $S$, il cui risultato è ordinato secondo un ordine significativo $O$ e il cui costo è maggiore di quello di un piano $AP^{'}$ per le stesse relazioni e con lo stesso ordine (o più significativo), non può essere esteso in un piano di accesso a costo minimo

si dice che $AP^{'}$ domina $AP$

Controllo del livello di ottimizzazione
#

DB2 permette di controllare il livello di ottimizzazione applicato alle query per mezzo del parametro

SET CURRENT QUERY OPTIMIZATION = n

dove $n$ può assumere i seguenti valori:

$0$ Basic rewrite rules, greedy join enumeration, only nested loops join
$1$ Frequent values statistics are not used, greedy join enumeration, subset of rewrite rules
$2$ All statistics are used, almost all rewrite rules are applied, greedy join enumeration
$3$ DP enumeration (left-deep & no Cartesian products), index ANDing
$5$ (default) More complex rewrite rules
$7$ Similar to 5 but without the heuristic rules
$9$ A maximal amount of optimization is performed to generate an access plan.

Gestione del group by
#

Nei DBMS moderni il group by viene gestito al termine dell’esecuzione dei join, tuttavia vi e la possibilità di farne il push down a patto che i valori delle funzioni aggregate non cambino