Nati per soddisfare query che coinvolgono molteplici attributi, tra cui
- query puntuali $A_1 = v_1, A_2 = v_2, … , A_n = v_n$
- query finestra $l_1 \leq A_1 \leq h_0, l_2 \leq A_2 \leq h_2, … , l_n \leq A_n \leq h_n$
- nearest neighbor query $A_1 \approx v_1, A_2 \approx v_2, … , A_n \approx v_n$
Limiti del b+tree #
Supponendo di avere una window query su due attributi $A,B$ del tipo
SELECT * FROM table as T
WHERE T.A > 10
AND T.A < 20
AND T.B > 10
AND T.B < 20
In questo caso e possibile utilizzare un indice b+tree su entrambi gli attributi oppure 2 indici monodimensionali su i due attributi
In entrambi i casi si compie del lavoro inutile perché i punti spazialmente vicini non sono posti nelle stesse foglie
Indicizzamento spaziale #
Per affrontare il problema sono state proposte una marea di strutture dati ma il concetto resta lo stesso, mappare record spazialmente vicini nelle stesse pagine
K-d-tree #
Struttura mantenuta in memoria centrale non paginata e non bilanciata, dove ogni nodo rappresenta uno split sul valore mediana dell’attributo con la maggiore varianza
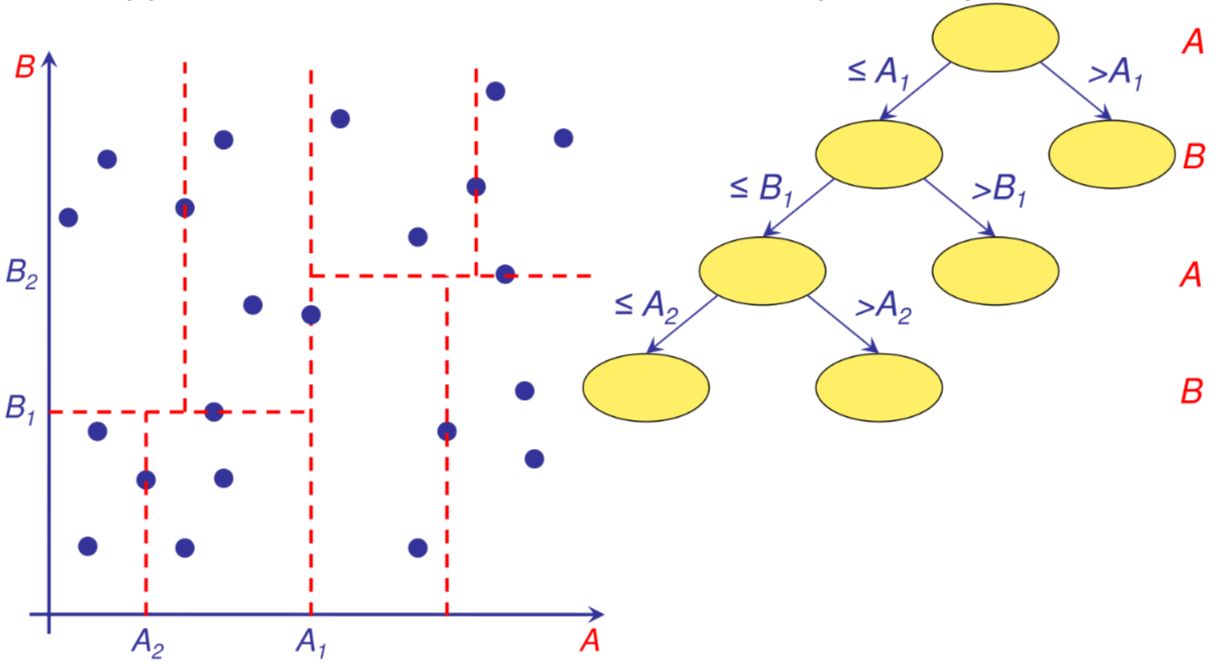
K-d-tree ricerca #
In caso di ricerca si visitano tutti i rami dell’albero che contengono regioni che si intersecano con la regione definita dalla query
❗ dato che l’albero non e bilanciato sono necessarie operazioni di ribilanciamento periodiche
le eliminazioni sono estremamente complicate
Paginando il k-d-tree: k-d-b-tree #
E la versione paginata del K-d-tree dove ogni nodo corrisponde a un iper-rettangolo dello spazio ottenuto come unione delle regioni figlie
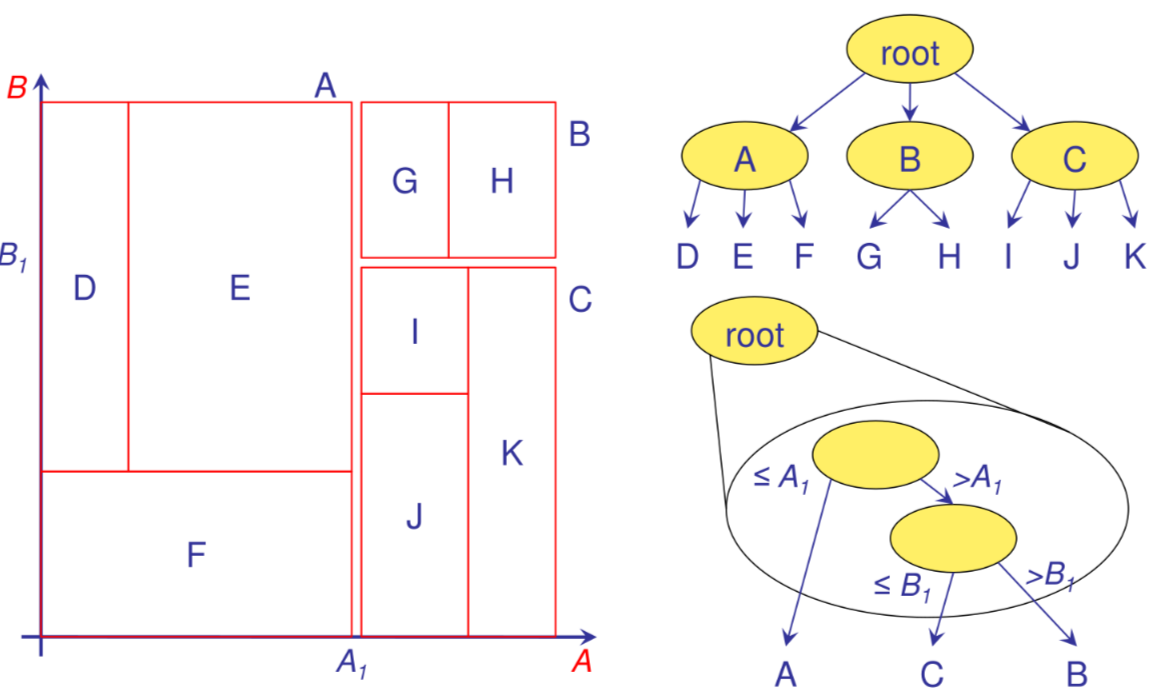
K-d-b-tree: overflow #
In caso di overflow si partizionano i nodi padri fino a risalire alla root
❗ non e sempre possibile mantenere il bilanciamento durante l’operazione di split
hB-tree #
Variante del k-d-B-tree in cui le regioni possono contenere buchi, questo migliora la situazione in caso di split di un data block la differenza e data dal fatto che un nodo può essere referenziato da più separazioni

hB-tree: split #
In caso di split della root i nodi figli vengono splittati come segue
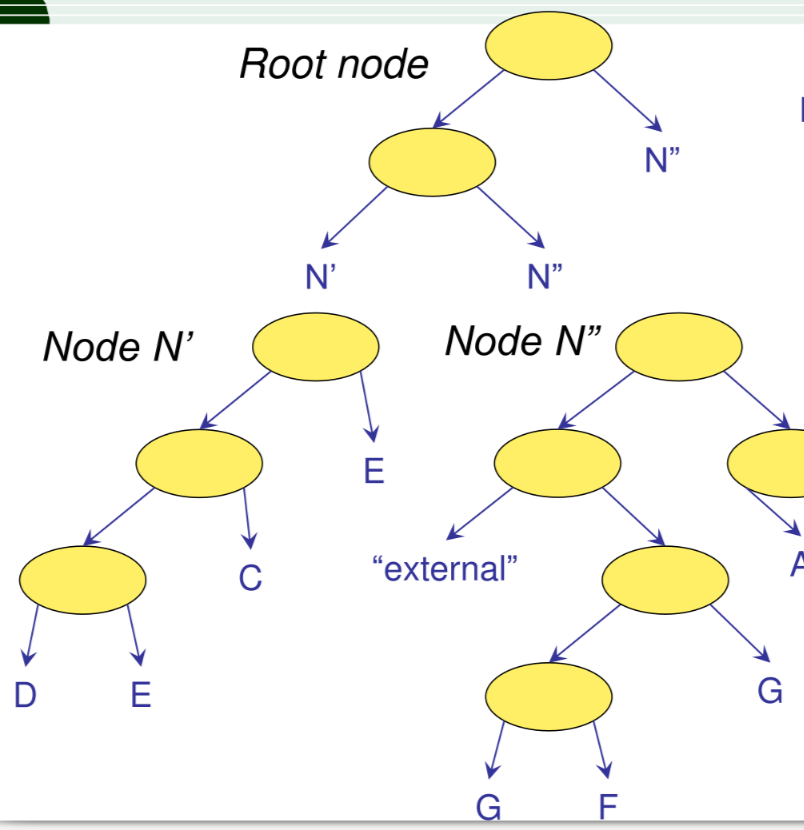
Excell #
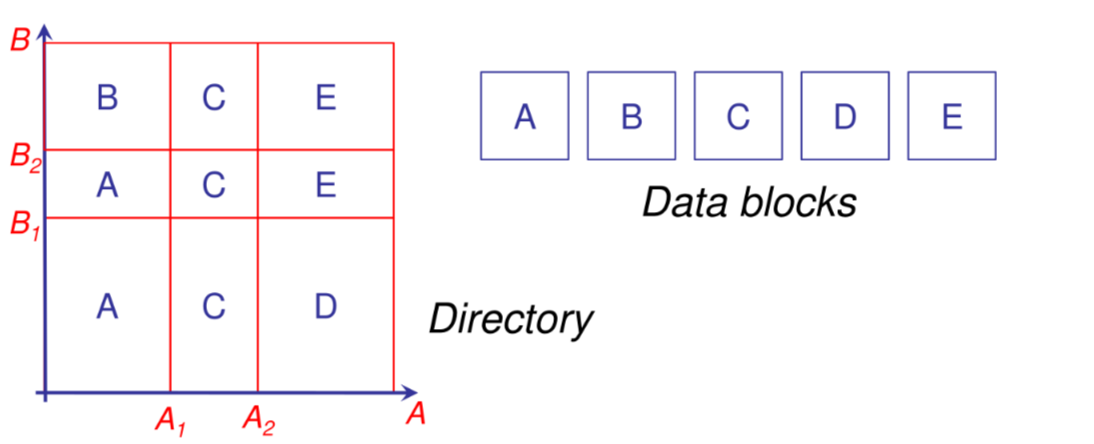
Tecnica basata su una hash directory fatta a griglia $n$-dimensionale dove ogni cella corrisponde a una datapage ma non e vero il contrario, estendendo il concetto di extendible hashing al caso multidimensionale.
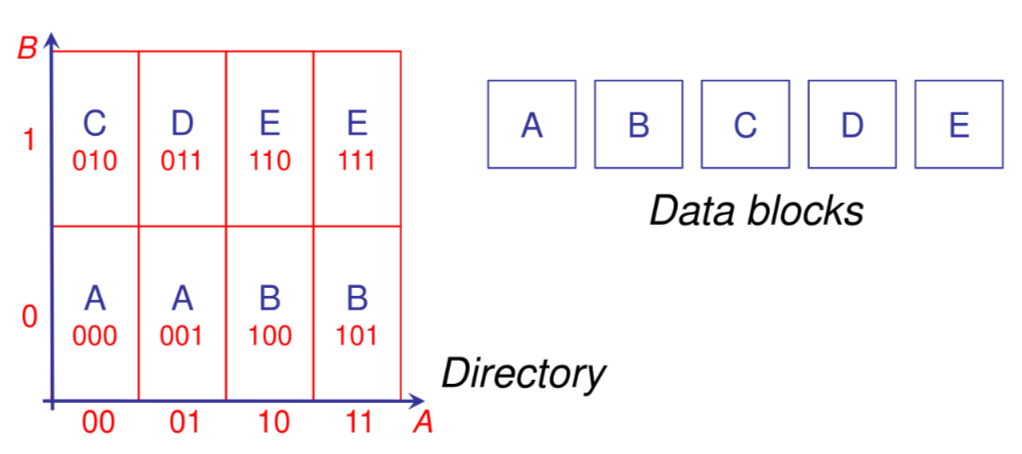
Excell: split #
In caso di split ci sono due casistiche:
- split di una datapage referenziata da due celle della directory, in questo caso e sufficiente aggiornare le referenze della directory
- split di una datapage referenziata da una cella della directory in questo caso si raddoppia la dimensione della griglia
ℹ️ tutte le problematiche e considerazioni fatte per l’
href="/tecnologie_basi_dati/indici_hash#extendible-hashing">extendible hashing
restano valide
Grid file #
Versione generalizzata del Excell, dove gli intervalli hanno dimensione variabile,
Mono-dimensional sorting #
Si basa sul concetto di linearizzare lo spazio n dimensionale per mezzo delle cosiddette space-filling curves
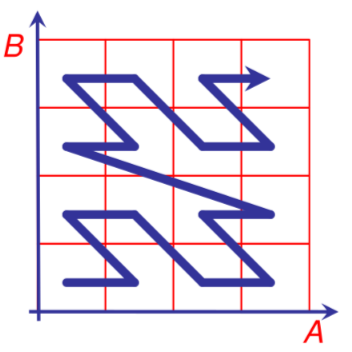
In questo caso preservare l’ordine locale risulta quasi impossibile
